105. Construct Binary Tree from Preorder and Inorder Traversal

Description

See: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal

We are given two arrays as inputs, one containing the preorder traversal of a tree and one containing the inorder traversal of the same tree. Our task is to recreate the tree structure given those inputs.

Solution

The problem gives as an example:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]

The expected tree structure is:

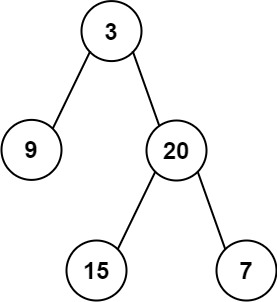
Observations

  • Preorder traversal processes the tree in order: Node -> Left -> Right

  • Inorder traversal processes the tree in order: Left -> Node -> Right

  • From these two facts come the following observations:

    • The first element in the preorder array will always be the root node of the tree.

    • In the inorder array, elements to the left of the node will form the left side of the tree. Elements to the right of the node will form the right side of the tree.

  • Trees and traversal use recursion for an elegant solution. Using the top-down recursive strategy we can break the problem into subproblems.

    • In this case we want to create subtrees in order to build the entire tree.

    • Imagining the function already exists, I would want to do something like

node.left = make_tree()
node.right = make_tree()

  • The first two facts and observations are true for the subtrees, but with subportions of the preorder and inorder arrays.

Example walk through

From the preorder array [3,9,20,15,7], the root node is the first element, which is 3.

In the inorder array [9,3,15,20,7], items to the left of 3 are the left subtree. Items to the right of 3 are the right subtree. So, 9 is the left side subtree. 15, 20 and 7 form the right side subtree.

We can think of the tree structure as the following diagram.

We know 3 is the root, we need to form the left and right subtrees to complete the tree. We know there will be something on the left and something on the right, but we do not know its structure yet. We will break the creation of the left and right subtrees into subproblems.

To form the left subtree, we get the next element from the preorder array which is 9. This is the root node for the left subtree. We will only use a portion of the inorder array, since we only want those elements that are children of node 9. Looking at the inorder array, [9,3,15,20,7], there are no elements to the left of 9. So, it has no left children. The items to the right of 9 are not part of its children because 3 is the root. So, 9 has no right children. We can think of the tree structure now as:

We now get the next element of the preorder array, [3,9,20,15,7], which is 20. 20 is the root of the right side subtree. Again, we will only use a portion of the inorder array, since we only want those elements that are children of node 20. Looking at the inorder array, [9,3,15,20,7], there is one element to the left of 20 which has not been used, 15. It is the root node of that left subtree. There is one element to the left of 20, 7. It is the root of that right subtree. We can think of the tree structure now as:

We now get the next element of the preorder array, [3,9,20,15,7], which is 15. 15 is the root of the left side subtree. Again, we will only use a portion of the inorder array, since we only want those elements that are children of node 15. Looking at the inorder array, [9,3,15,20,7], there are no elements to the left of 15 which have not been used. There are also no elements to the right of 15 that have not been used. So, 15 has no children. We can think of the tree structure now as:

We now get the next element of the preorder array, [3,9,20,15,7], which is 7. 7 is the root of the right side subtree. Again, we will only use a portion of the inorder array, since we only want those elements that are children of node 7. Looking at the inorder array, [9,3,15,20,7], there are no elements to the left of 7 which have not been used. There are also no elements to the right of 7 as we've reached the end of the array. So, 7 has no children. The tree has now been formed:

Code

From the above walk through we will need to keep track of the following:

  • the index of the elements in the inorder array

    • We will need to look up the position of the root node in the inorder array. Indexes less than the node index will be left children. Indexes that are greater than the node index will be right children. We can store each element's index in a dict to make look up easy.

  • the current range of indexes to use in the inorder array

    • we can keep track of the start and end indexes to use in the inorder array.

    • For the left side, the indexes to use will be from the start -> node index - 1

    • For the right side, the indexes to use will be from node index + 1 -> end

    • For the root node, the entire inorder array will be used. So, the start will be 0 and end will be len(inorder) - 1 (4 in this example)

      • In this example, when the root node passes in the bounds for the left and right subtrees the indexes will be:

        • left: start: 0 end: 0

        • right: start: 2 end: 4

  • the current element in the preorder array

    • Keep track of this at the class level, as we do not want to recursively get the preorder array elements. We just want to iterate through them.

class Solution:

    def __init__(self):
        # The index of the preorder array element currently being processed
        self.preorder_index = 0

    def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
        def make_tree(start, end):
            """
            :param start: the index to start at in the inorder array
            :param end: the index to end at in the inorder array
            :return: the TreeNode structure or None if the end index is less than the start index
            """
            if end < start:
                return None
            root = TreeNode(preorder[self.preorder_index])
            self.preorder_index += 1
            root_index = location[root.val]
            root.left = make_tree(start, root_index - 1)
            root.right = make_tree(root_index + 1, end)
            return root

        # set self.preorder_index to 0 in case the buildTree method is called multiple times on the Solution instance.
        # If it wasn't set then the self.preorder_index would be a value used in the previous invocation.
        self.preorder_index = 0
        location = {}
        for index, value in enumerate(inorder):
            location[value] = index
        return make_tree(0, len(inorder) - 1)

Time complexity: O(N)

Space complexity: O(N)

Previous98. Validate Binary Search TreeNext121. Best Time to Buy and Sell Stock

Last updated